Welcome

MagIC is a numerical code that can simulate fluid dynamics in a spherical shell. MagIC solves for the Navier-Stokes equation including Coriolis force, optionally coupled with an induction equation for Magneto-Hydro Dynamics (MHD), a temperature (or entropy) equation and an equation for chemical composition under both the anelastic and the Boussinesq approximations.

MagIC uses Chebyshev polynomials or finite difference in the radial direction and spherical harmonic decomposition in the azimuthal and latitudinal directions. MagIC supports several Implicit-Explicit time schemes where the nonlinear terms and the Coriolis force are treated explicitly, while the remaining linear terms are treated implicitly.

MagIC is written in Fortran and designed to be used on supercomputing clusters. It thus relies on a hybrid parallelisation scheme using both OpenMP and MPI. Postprocessing functions written in python (requiring matplotlib and scipy) are also provided to allow a useful data analysis.

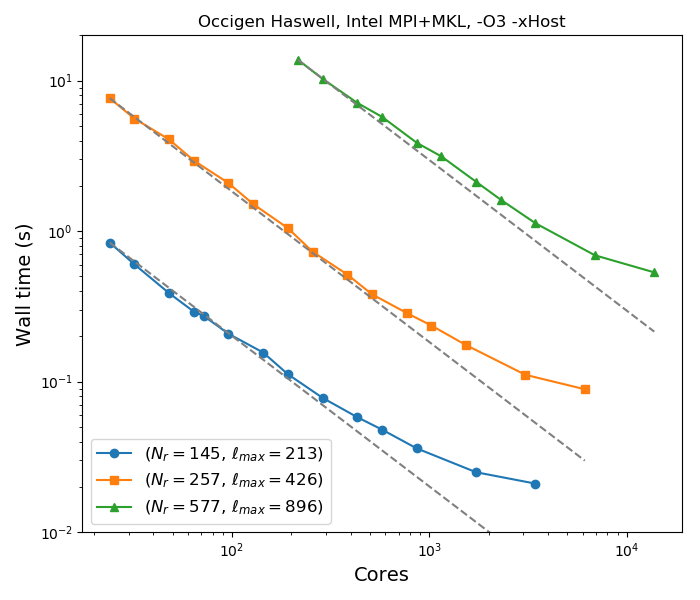
Walltime of MagIC on Occigen versus number of cores for a Boussinesq dynamo model computed at three different numerical resolutions \((N_r,\ell_{\text{max}})\).

MagIC is a free software. It can be used, modified and redistributed under the terms of the GNU GPL v3 licence.

Quickly starting using MagIC

• The quick-starting guide will help you to download, set up and run your first numerical simulations using MagIC.

• The description of the input namelists will then help you to define the exact physical setup you may want to simulate.

• The description of the output files will help you to understand what are the diagnostic quantities computed by MagIC.

• Finally, the python functions and classes will allow you to do some advanced post-processing analyses on the outputs of MagIC.

Documentation

• The table of contents gives an overview of the complete documentation.

• The formulation of the (M)HD problem contains an exhaustive description of the equations solved by the MagIC code.

• The numerical methods section contains the description of the numerical technique.

• The search page allows to search the documentation.

• The fortran API contains a generic description of all Fortran variables, subroutines and modules used in MagIC.

You can also download a PDF version of this documentation generated from LaTeX Sphinx.

Contributing to the code

If you want to contribute to MagIC, the contributor guide might be helpful for you.

Giving credit

In case you intend to publish scientific results obtained with MagIC or present them in a conference, we (the developers of MagIC) kindly ask to be acknowledged with a reference to the website https://magic-sph.github.io/ or https://github.com/magic-sph/magic.

We also suggest to give appropriate reference to one or several of the following papers:

• Boussinesq equations: Wicht (2002, PEPI, 132, 281-302)

• Anelastic equations: Gastine & Wicht (2012, Icarus, 219, 28-442)

• Boussinesq benchmark: Christensen et al. (2001, PEPI, 128, 25-34)

• Benchmark for double diffusive convection: Breuer et al. (2010, GJI, 183, 150-162)

• Anelastic benchmark: Jones et al. (2011, Icarus, 216, 120-135)

• In case you use the SHTns library for the spherical harmonics transforms (MagIC 5.3 or later), please also cite: Schaeffer (2013, GGG, 14, 751-758)

See also

A (tentative) comprehensive list of the publications that have been produced to date (May 2024) using MagIC is accessible here. To date, more than 150 publications have been-accepted in more than 20 different peer-reviewed journals: PEPI (25), Icarus (15), E&PSL (7), GJI (17), A&A (16), GRL (7), JFM (7), GAFD (3), Nature (2), etc.

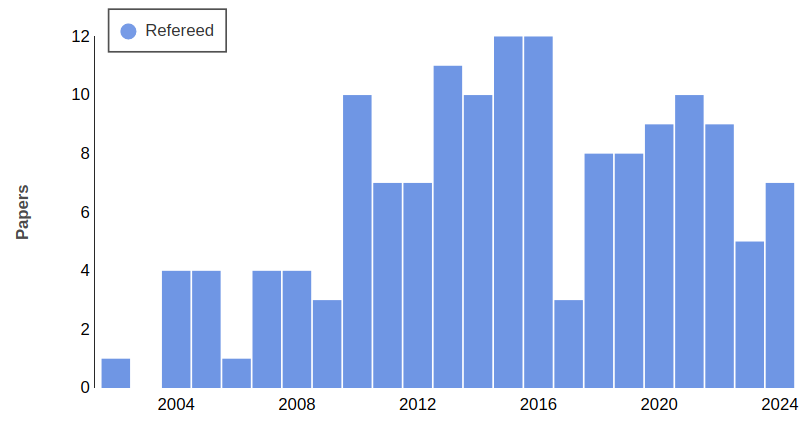
Number of peer-reviewed publications produced using MagIC